Introduction to Two Pointers Pattern
Two Pointers Pattern
The Two Pointers pattern is a powerful technique used to solve problems that involve finding relationships between elements in an array, string, or linked list.
Instead of using nested loops (
When to Use
- Array or string is sorted
- You need to compare or combine elements from different positions
- You want to shrink/expand a window over the data
- You need in-place rearrangement without extra memory
- You’re working with linked lists for middle/cycle detection
Main Variants
We’ll go through 6 core types of two pointer patterns, each with:
- Explanation
- Example
- Key LeetCode problems
1. Opposite Direction Pointers (Start–End)
When to Use
- Sorted arrays / strings
- Need to find a pair/triplet with specific sum/difference
- Symmetry checks (palindromes, mirrored data)
How It Works
- One pointer starts at the beginning (
left), the other at the end (right) - Compare the values and move pointers based on condition
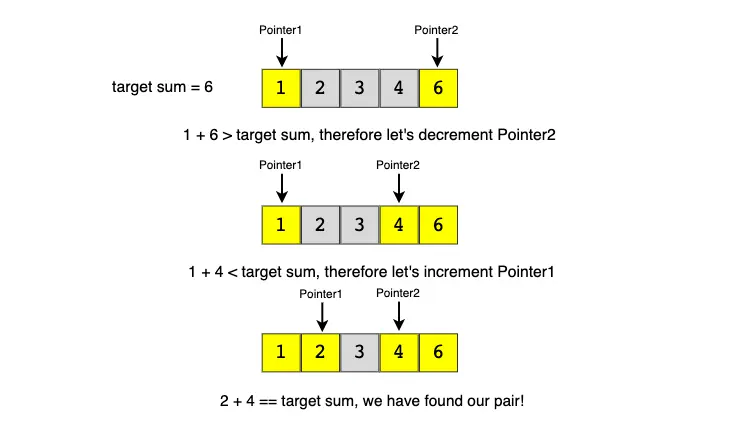
Example
Problem: Given a sorted array, find a pair that adds to a target sum.
Pseudocode:
def two_sum_sorted(arr, target):
left, right = 0, len(arr) - 1
while left < right:
total = arr[left] + arr[right]
if total == target:
return [left, right]
elif total < target:
left += 1
else:
right -= 1
return []
Complexity:
LeetCode Examples:
-
- Container With Most Water
-
- Trapping Rain Water (optimized)
2. Same Direction Pointers (Sliding Window)
When to Use
- Substring/subarray problems
- Need to maintain a window of elements that meets a condition
How It Works
- Both pointers start at the same position
- Move
rightto expand the window - Move
leftto shrink when a condition is violated
Example
Problem: Longest substring without repeating characters.
def length_of_longest_substring(s):
left = 0
seen = {}
max_len = 0
for right in range(len(s)):
if s[right] in seen and seen[s[right]] >= left:
left = seen[s[right]] + 1
seen[s[right]] = right
max_len = max(max_len, right - left + 1)
return max_len
Complexity:
LeetCode Examples:
-
- Longest Substring Without Repeating Characters
-
- Minimum Size Subarray Sum
-
- Fruit Into Baskets
-
- Minimum Window Substring
3. Fast & Slow Pointers (Tortoise–Hare)
A two pointer algorithm where pointers move at different speeds. By moving at different speeds (say, in a cyclic LinkedList), the algorithm proves that the two pointers are bound to meet. The fast pointer should catch the slow pointer once both the pointers are in a cyclic loop. Commonly, the “fast” pointer moves two steps at a time, while the “slow” pointer moves one step at a time.
Example Scenario
Imagine two friends walking around a circular track:
- One friend (the “slow” pointer) walks one lap per hour.
- Another friend (the “fast” pointer) runs two laps per hour. If there is a cycle (the track is circular), the fast pointer will eventually “lap” or catch up to the slow pointer. This concept directly translates to data structures where pointers traverse nodes.
When to Use
- Cycle detection: The pattern helps in detecting cycles without extra space. You don’t need additional data structures like hash sets to keep track of visited nodes.
- Finding middle of linked list: Using different movement speeds allows you to pinpoint interesting locations, such as the middle of a list or the start of a cycle.
- Detecting repeats
Key Scenarios Where This Pattern Shines
- Linked List Cycle Detection: Whenever a problem states, “Given a linked list, determine if it has a cycle,” you should think about the Fast & Slow Pointers pattern.
- Middle of a Linked List: If you need to find the middle node of a list in one pass, the Fast & Slow Pointers approach is perfect.
- Length of a Cycle: After detecting a cycle, you can continue with the fast pointer to measure the cycle length.
- Reorder or Split Linked List: When partitioning or rearranging a linked list, finding the middle node is often crucial.
How It Works
slowmoves 1 step at a timefastmoves 2 steps- If they meet, there’s a cycle
- If
fastreaches the end, no cycle
Example
Problem: Detect cycle in a linked list.
def has_cycle(head):
slow, fast = head, head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
Complexity:
LeetCode Examples:
-
- Linked List Cycle II
-
- Middle of the Linked List
-
- Happy Number
4. Partitioning Pointers
When to Use
- In-place reordering without extra memory
- Partitioning elements based on condition
How It Works
- Maintain two pointers, one tracking processed elements and the other scanning
- Swap when condition is met
Example
Problem: Move zeroes to end.
def move_zeroes(nums):
insert_pos = 0
for num in nums:
if num != 0:
nums[insert_pos] = num
insert_pos += 1
for i in range(insert_pos, len(nums)):
nums[i] = 0
LeetCode Examples:
-
- Move Zeroes
-
- Sort Colors (Dutch National Flag problem)
-
- Partition List
5. K-Distance Apart
When to Use
- Linked list problems where you need N-th node from end
- Maintaining a gap of k between pointers
How It Works
- Move the first pointer k steps ahead
- Move both pointers together until the first reaches the end
Example
Problem: Remove N-th node from end of list.
def remove_nth_from_end(head, n):
dummy = ListNode(0, head)
first = second = dummy
for _ in range(n+1):
first = first.next
while first:
first = first.next
second = second.next
second.next = second.next.next
return dummy.next
LeetCode Examples:
-
- Remove Nth Node From End of List
-
- Reverse Nodes in k-Group
6. Merge-Style Pointers
When to Use
- Merging sorted arrays/lists
- Finding intersections or overlaps
How It Works
- One pointer for each sorted sequence
- Advance pointer with smaller value
Example
Problem: Merge two sorted lists.
def merge_two_lists(l1, l2):
dummy = ListNode()
tail = dummy
while l1 and l2:
if l1.val < l2.val:
tail.next, l1 = l1, l1.next
else:
tail.next, l2 = l2, l2.next
tail = tail.next
tail.next = l1 or l2
return dummy.next
LeetCode Examples:
-
- Merge Two Sorted Lists
-
- Merge Intervals
-
- Merge Sorted Array
-
- Intersection of Two Arrays II
Quick Decision Table
| Problem Type | Recommended Pattern |
|---|---|
| Sorted + sum/diff check | Opposite Direction |
| Sorted + merging/intersection | Merge-Style |
| Subarray/substring constraint | Sliding Window |
| Linked list cycle/middle | Fast & Slow |
| N-th from end | K-Distance Apart |
| In-place reorder | Partitioning |