Two Pointers

• Uses two pointers to traverse an array or a list from different ends or directions
• Useful when given a sorted array and need to look into each element possibly in pair
• Two Pointers

def findTarget(arr, target_sum):
    left, right = 0, len(arr) - 1
    while(left < right):
      current_sum = arr[left] + arr[right]
      if current_sum == target_sum:
        return [left, right]

      if target_sum > current_sum:
        left += 1  # we need a pair with a bigger sum
      else:
        right -= 1  # we need a pair with a smaller sum
    return [-1, -1]

Fast & Slow Pointers

• Uses two pointers which move at different speeds

def hasCycle(self, head):
  slow, fast = head, head # start at the same place
  while fast != None and fast.next:
    fast = fast.next.next # fast pointer moves 2x
    slow = slow.next # slow pointer moves at regular speed
    if slow == fast: # if they meet we found a cycle
      return True
  return False

Sliding Window

• Uses two pointers to maintain the edges of the window
• Useful when trying to find something from all sub-arrays

Fixed Size Window

def findAverages(self, K, arr):
    result = []
    windowSum, windowStart = 0.0, 0
    for windowEnd in range(len(arr)):
        windowSum += arr[windowEnd]  # add the next element
        # slide the window, no need to slide
        # if we've not hit the required window size of 'k'
        if windowEnd >= K - 1:
            result.append(windowSum / K)  # calculate the average
            windowSum -= arr[windowStart]  # subtract the element going out
            windowStart += 1  # slide the window ahead
    return result

Variable Size Window

def longestSubarray(self, nums):
	result = 0
	L = 0
	for R in range(len(nums)):
		if nums[L] != nums[R]:
			L = R
		result = max(result, R - L + 1)
	return result

def shortestSubarray(nums, target):
	L, total = 0, 0
	length = float('-inf')

	for R in range(len(nums)):
		total += nums[R]
		while total >= target:
			length = min(length, R - L + 1)
			total -= nums[L]
			L += 1
	return 0 if length == float('inf') else length

Prefix Sum

• TODO

Merge Intervals

• Uses sorting to preprocess the array
• Keep a previous start and end and adds it once the current does not overlap
• For current, we just need to check whether the start is equal or before the prev's end

def merge(self, intervals):
  # sort the intervals on the start time
  intervals.sort(key=lambda x: x.start)

  mergedIntervals = []
  start = intervals[0].start
  end = intervals[0].end
  for i in range(1, len(intervals)):
    interval = intervals[i]
    if interval.start <= end:  # overlapping intervals, adjust the 'end'
      end = max(interval.end, end)
    else:  # non-overlapping interval, add the previous interval and reset
      mergedIntervals.append(Interval(start, end))
      start = interval.start
      end = interval.end

  # add the last interval
  mergedIntervals.append(Interval(start, end))
  return mergedIntervals

Cyclic Sort

• Uses pointer and swaps current value with its pre-determined right place

def sort(self, nums):
  i = 0
  while i < len(nums):
    j = nums[i] - 1  # the correct index of the current num
    if nums[i] != nums[j]: # check if current num is at the wrong place
      nums[i], nums[j] = nums[j], nums[i]  # swap with its right place
    else:
      i += 1  # move forward if already at the right place
  return nums

In-place Reversal of a Linked List

• Useful when have to do an in-place reversal without using extra memory

def reverse(self, head):
    previous, current, next = None, head, None
    while current is not None:
        next = current.next  # temporarily store the next node
        current.next = previous  # reverse the current node
        # before we move to the next node, point previous to the current node
        previous = current
        current = next  # move on the next node
    return previous

Stack

• Useful when Last item added is to be processed first

def isValidParentheses(self, s):
    stack = []
    # key = closing
    # value = opening
    matching = {"}": "{", "]": "[", ")": "("}
    opening = {"(", "[", "{"}
    closing = {")", "]", "}"}
    for char in s:
        if char in opening:
            stack.append(char)
        else:
            # has to be a closing bracket
            # check whether it matches with the last item in stack
            if stack[-1] != matching[char]:
                return False
            else:
                stack.pop()
    return True

Depth First Search (DFS) - Tree Traversals

Tree to be used for showing traversal outputs

       1
      / \
     2   3
    / \
   4   5

Pre order

# prints 1, 2, 4, 5, 3
def preorder(root: TreeNode) -> None:
    if not root: return
    print(root.val)
    preorder(root.left)
    preorder(root.right)

In order

• can be used to print in sorted order a BST

# prints 4, 2, 5, 1, 3
def inorder(root: TreeNode) -> None:
    if not root: return
    inorder(root.left)
    print(root.val)
    inorder(root.right)

Post order

# prints 4, 5, 2, 3, 1
def postorder(root: TreeNode) -> None:
    if not root: return
    postorder(root.left)
    postorder(root.right)
    print(root.val)

Breadth First Search (BFS)

• Uses Queue
• Add root to the initial queue and q.popleft() to pop items
• Process current node and then push its children to the queue
• If you need to process per level then use a for _ in range(len(q))

Level order Tree Traversal

# prints 1, 2, 3, 4, 5
def levelorder(root: TreeNode) -> None:
    if not root: return
    q = deque([root])
    
    while q:
        size = len(q)
        for i in range(size):
            node = q.popleft()
            print(str(node.val), end = " ")
            if node.left: 
                q.append(node.left)
            if node.right: 
                q.append(node.right)

        print()

BFS for Graph (Queue)

Exactly the same as DFS but with queue instead of stack

def BFS(self, startVertex):
    visited = [False] * self.V  # To keep track of visited vertices
    q = deque()

    visited[startVertex] = True
    q.append(startVertex)

    while q:
        currentVertex = q.popleft()
        print(currentVertex, end=" ")

        # Explore adjacent vertices
        for neighbor in self.adjList[currentVertex]:
            if not visited[neighbor]:
                q.append(neighbor)
                visited[neighbor] = True

Depth First Search (DFS)

• Recursion or Stack
• Ensure you check for edge cases like root is None

DFS for Trees (Recursive)

def mainFunction(root):
	return self.recursiveFunction(root)

def recursiveFunction(self, currentNode):
	# sanity check - return falsy or empty value here
	if currentNode is None:
		return False
	# base case - smallest problem or dealing with leaf node
	if currentNode.left is None and currentNode.right is None and ...:
		return ...

	# recursive case - call the recursive function with left and right child
	# and a smaller data
	return self.recursiveFunction(currentNode.left) or self.recursiveFunction(currentNode.right)

DFS for Trees (Stacks)

def dfs(root):
	if not root:
		return
	stack = [root]
	while stack:
		node = stack.pop()
		# do something with node to process it
		if node.left:
			stack.append(node.left)
		if node.right:
			stack.append(node.right)

DFS for Graph (Recursive)

def validPath(self, n: int, edges: [[int]], start: int, end: int) -> bool:
	# Need this for any graph algorithm
	visited = set()

	# IF need to convert List of edges to adjacency matrix
	graph = defaultdict(list)
	for v1, v2 in edges:
		graph[v1].append(v2)
		graph[v2].append(v1)

	# the recursive function
	def dfs(root):
		# base case
		if root == end:
			return True

		visited.add(root)

		for neighbor in graph[root]:
			if neighbor not in visited and dfs(neighbor):
				return True
		return False
	return dfs(start)

DFS for Graph (Stack)

def DFS(self, start):
    visited = [False] * self.vertices # this or a dict
    
    stack = [] 
    stack.append(start)
    visited[start] = True

    while stack:
        curr = stack.pop()
        print(curr) # process the current node

		# Add all the adjacent vertices
        for neighbor in self.adjList[curr]:
            if not visited[neighbor]:
                stack.append(neighbor)
                visited[neighbor] = True

Matrix Traversal

• Loop over each row, column and BFS/DFS from the first valid cell
• Maintain a visited matrix
• Add valid neighbouring cells to queue/stack

Two Heaps

• Two heaps are used simultaneously (min and max heaps)
• Used when a set of elements can be divided into two parts

Subsets

• Solves Permutations and Combinations problems
• Uses BFS with a queue
• Time: $O(n\ast 2^n)$

Generate Subsets (Iterative)

def findSubsets(self, nums):
  subsets = []
  # start by adding the empty subset
  subsets.append([])
  for currentNumber in nums:
    # we will take all existing subsets and 
    # insert the current number in them to create 
    # new subsets
    n = len(subsets)
    for i in range(n):
      # create a new subset from the existing subset and insert the current element to it
      set1 = list(subsets[i])
      set1.append(currentNumber)
      subsets.append(set1)

  return subsets

Generate Subsets (Recursive)

Unique Values

def subsets(self, nums: List[int]) -> List[List[int]]:
	result, current = [], []
	self.decisionTree(0, nums, result, current)
	return result

def decisionTree(self, i, nums, result, current):
	# base case - out of bounds
	# add our current subset to results
	if i == len(nums):
		return result.append(current.copy())

	# first decision - include i in subset
	current.append(nums[i])
	self.decisionTree(i + 1, nums, result, current)

	# second decision - do not include i in subset
	current.pop()
	self.decisionTree(i + 1, nums, result, current)

Duplicate Values

def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
	# Difference 1 - Sort because need to skip duplicates
	nums.sort()
	i, nums, result, current = 0, nums, [], []
	self.generateSubsets(i, nums, result, current)
	return result

def generateSubsets(self, i, nums, result, current):
	if i == len(nums):
		return result.append(current.copy())

	# first decision - include nums[i]
	current.append(nums[i])
	self.generateSubsets(i + 1, nums, result, current)

	# second decision - do not include all numbers of nums[i]
	current.pop()
	
	# Difference 2 - Skip all duplicates 
	while i + 1 < len(nums) and nums[i] == nums[i + 1]:
		i += 1

	self.generateSubsets(i + 1, nums, result, current)

Combinations

• $(\genfrac{}{}{0ex}{}{n}{k})=\frac{n!}{k!(n-k)!}$
• Similar to subset but another base case of i > n - used where we go the route of empty sets
• Time Complexity: $O(k\ast n^k)$

Similar to Subsets

def combine(self, n: int, k: int) -> List[List[int]]:
	current, result = [], []
	self.generateCombinations(1, n, k, current, result)
	return result

def generateCombinations(self, i, n, k, current, result):
	# base case 1: have generated the required number of combinations
	if len(current) == k:
		return result.append(current.copy())

	# have gone over n
	if i > n:
		return

	# decision 1: include i in combination
	current.append(i)
	self.generateCombinations(i + 1, n, k, current, result)

	# decision 2: do NOT include i in combination
	current.pop()
	self.generateCombinations(i + 1, n, k, current, result)

Alternative

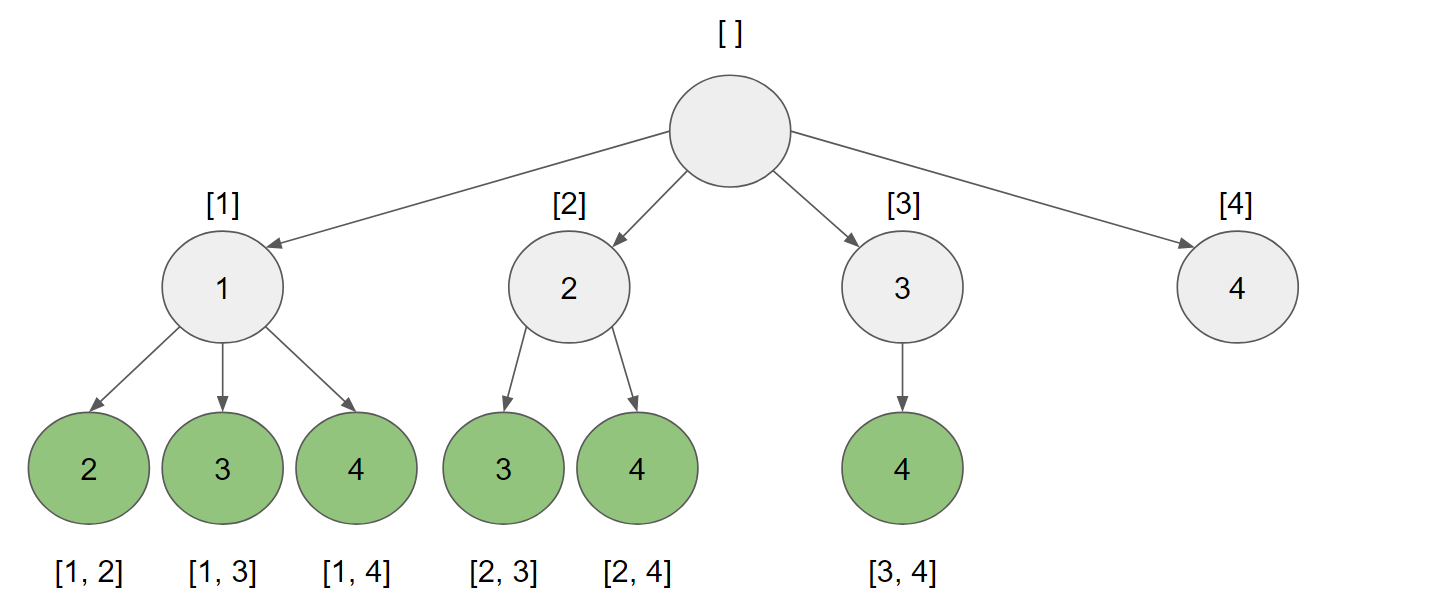
def combine(self, n: int, k: int) -> List[List[int]]:
	current, result = [], []

	def generate(index):
		if len(current) == k: # have added the required number of items within our combination
			result.append(current.copy())
			return

		if index > n:
			return

		for i in range(index, n + 1):
			current.append(i) # include the current number
			generate(i + 1) # generate combinations from it
			current.pop() # do not include the current number, will work in the next iteration
	
	generate(1)
	return result

Permutations

Recursive

def permute(self, nums: List[int]) -> List[List[int]]:
	current, result = [], []
	self.generatePerms(nums, current, result)
	return result

def generatePerms(self, nums, current, result):
	if len(current) == len(nums):
		return result.append(current.copy())
	
	for num in nums:
		if num not in current:
			current.append(num)
			self.generatePerms(nums, current, result)
			current.pop()

Iterative

def permutations(nums):
	return generatePerms(0, nums)
def generatePerms(i, nums):
	if i == len(nums):
		return [[]]

	result = []
	perms = generatePerms(i + 1, nums)
	for p in perms:
		for j in range(len(p) + 1):
			copy = p.copy()
			pCopy.insert(j, nums[i])
			result.append(copy)
	return result

Binary Search

• Should be used when given a sorted Array and asked to find some element

start, end = 0, len(arr) - 1

# always less and equal to
while start <= end:
  middle = start + (end - start) // 2 # avoids overflow 

  if arr[middle] < target: # search right
	start = middle + 1
  elif arr[middle] > target: # search left
	end = middle - 1 
  else:
	return middle # found it

XOR

• Used to find a missing value in a range when summing, without integer overflow
• XOR of a number with itself is 0
• XOR of a number with 0 gives the number back
• XOR is both associative and commutative
• XOR in Python result = variable1 ^ variable2

# every number in arr is twice except one - find that one number
result = 0
for num in arr:
  result ^= num # XOR two same numbers makes it a 0 - single num remains
return result

Top K Elements

• Use Heap for Top K smallest, largest or frequent elements
• Used when given an unsorted list

from heapq import *
def findKLargestNumbers(self, nums, k):
  heap = [] # simple list
  for num in nums:
    if len(heap) < k: # maintain only *k* elements in the min heap
      heappush(heap, num)
    else:
	  # if you find larger number than minHeap root, replace it
      if num > heap[0]:
        heappop(heap)
        heappush(heap, num)
  return heap

Quickselect

• Used to find $k^{th}$ smallest / largest / most frequent / less frequent
• Average time complexity of $O(N)$ but rare worst case is $O(N^2)$

K-way Merge

• Use Heap to traverse multiple sorted arrays
• Add first element from all arrays to the heap
• Pop the first element and add it to the result
• Add the next item from the popped element list

Kadane's Algorithm

• Used for maximum subarray problems
• Subarray is contiguous

Base Algorithm

• Looking for just the sum and not the indices

def maxSubArray(self, nums: List[int]) -> int:
	maxSum = nums[0] # assuming len(nums) > 0
	currentSum = 0 

	for num in nums:
		# discard previous negative subarray sum
		currentSum = max(currentSum, 0)

		# is new sum greater than best known sum
		currentSum += num
		maxSum = max(currentSum, maxSum)
	return maxSum

Sliding Window Variant

def maxSubArrayIndices(self, nums: List[int]) -> List[int, int]:
	current_sum, max_sum = 0, nums[0]
	start, max_start, max_end = 0, 0, 0

	for end, num in enumerate(nums):
		# If current sum is negative, reset it and set the new start index
		if current_sum < 0:
			current_sum = 0
			start = end

		current_sum += num
		
		# If the current sum exceeds the max sum, 
		# update max sum and subarray bounds
		if current_sum > max_sum:
			max_sum = current_sum
			max_start, max_end = start, end

	return [max_start, max_end]